IEEE-754浮点数那些坑：0.1加0.2不等于0.3！

浮点数是计算机程序中最基本的数据类型，几乎所有编程语言都有浮点类型。但你或许不知道，浮点数可能有精度不足的问题，使用不当会酿成大祸。以 JS 为例，我们来看一个例子：

1

0.1 + 0.2 === 0.3 // false

0.1 加上 0.2 居然不等于 0.3 ，那结果等于多少呢？

1

0.1 + 0.2 // 0.30000000000000004

结果等于一个非常接近 0.3 的值，但不等于 0.3 ！真是令人瞠目结舌！这是为什么呢？

想要回答这个问题，我们得知道浮点数在计算机内部是怎么表示的。IEEE 754 是目前使用最广泛的浮点数表示和运算标准，从中即可找到问题的答案。不过想要学习它之前，我们得先掌握 科学记数法 （ scientific notation ）。

科学计数法

在科学记数法中，一个数可以写成一个实数 a 和 10 的 n 次幂的积：$a\times10^n$ 。其中，

• n 必须是一个整数；
• $1 \le \left|a\right| \lt 10$ ，如果原数绝对值小于 1 或 大于等于 10 ，都可以通过改变 n 次幂来表示；

最后我们来看一些实际例子，应该不难理解：

IEEE 754

众所周知，计算机通常以二进制存储和处理数据，浮点数也不例外。那么，浮点数在计算机内部到底是如何存储的呢？这就是我们今天要学习的二进制浮点数算术标准—— IEEE 754 。

简而言之，IEEE 754 采用二进制版本的科学计数法来表示浮点数。

二进制浮点数

十进制数可以有小数点，二进制数也不例外，只是进制不同。十进制数第一位小数单位为 $10^{-1} = \frac{1}{10}$ ，即 0.1 ；类似地，二进制数第一位小数单位为 $2^{-1} = \frac{1}{2}$ ，即 0.5 。

请大家思考一个问题，二进制浮点数 1011.0101 换算成十进制应该是多少？不要看答案，自己先算一算。

我们把这个浮点数每一位的单位梳理一下，并换成十进制：

最后，将各个位对应的十进制值加起来，就得到最终结果：

$8+2+1+0.25+0.0625 = 11.3125$

二进制科学计数法

同样，二进制小数也能用科学计数法表示，只不过以 2 为幂。因为相邻二进制位之间相差 2 倍，而不是 10 倍。以上面例子为例，这个浮点数可以这样表示：

$1.0110101 \times 2^3$

IEEE 754 正是用这种方式来表示浮点数的！一个以科学计数法表示的浮点数，可以分为三个部分：

• 符号（ sign ），表示浮点数的正负，通常以 0 表示正，1 表示负；
• 小数（ fraction ），即例子中的 1.0110101 ，也叫作 有效数（ significand ）；
• 指数（ exponent ），表示 2 的 n 次幂，即例子中的 3 ；

同样，小数部分是一个绝对值大于等于 1，但小于 2 的数。如果浮点数小于 1 ，可以通过调整指数来表示。例如，0.011 可以表示成 $1.1 \times 2^{-2}$ 。

封装细节

IEEE 754 将这三部分封装到一组二进制位中，位数分为 32 位和 64 位两种不同版本。位数越多，可以表示的数值范围越大，精度越高。主流编程语言都使用 64 位版本，但我们以更简单的 32 位版本来讲解，原理都是一样的。

IEEE 754 32 位浮点数又称为单精度浮点数，由 32 个二进制位构成，其中：

• 符号（ sign ）占一位，第 31 位，0 表示正数，1 表示负数；
• 指数（ exponent ）占 8 位，第 23~30 位；
• 小数（ fraction ）占 23 位，第 0~22 位；

指数部分占 8 位，除去全零和全一表示特殊值，还剩 254 个值（ 1~254 ）。由于指数需要表示负数，IEEE 754 规定将指数和一个特殊的值，比如 127 相加后保存在这 8 位中。

• 第一个可用数值为 1 ，表示 -126 （ -126+127=1 ）；
• 最后一个可用数值为 254 ，表示 127 （ 127+127=254 ）；

由此可见，指数的表示范围为： -126~127 。

小数部分由于个位永远为 1 ，因此 IEEE 754 只保存小数点以后部分。举个例子，对于小数 1.0101 ，fraction 23 个二进制位分别保存 01010000000000000000000 。小数点前的 1 是固定的，不予保存。

最后，来看一个实际的例子：

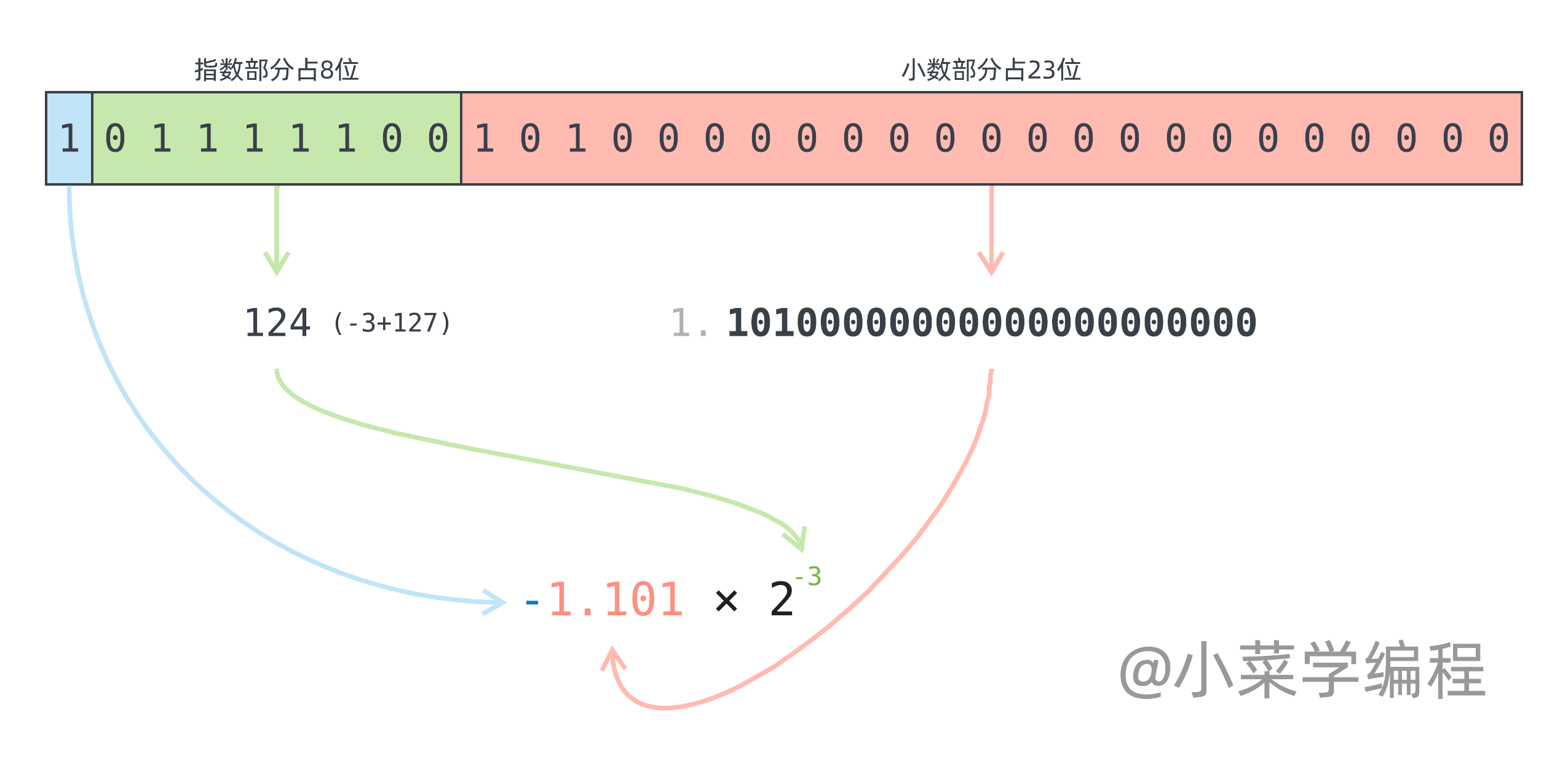
• 符号位决定符号，值为 1 说明这是一个负数；
• 指数部分数值为 124 ，实际指数需要再减去 127 ，得到：-3 ；
• 小数部分需要加上固定个位（ 1 ），得到：1.10100000000000000000000 ；

因此，实际保存的浮点数是 $-1.101 \times 2 ^ {-3}$ ，算一算十进制等于多少？—— $-0.203125$ ，不知您算对了没？

精度问题

那为什么用二进制科学计数法表示的浮点数，会有精度问题呢？

原因很简单——有些数无法用 2 的 n 次幂准确表示。举个例子，十进制浮点数 0.1 用二进制来表示，小数部分是无穷无尽的，只能不断逼近。以 32 位 IEEE 754 浮点数表示，结果如下：

$1.10011001100110011001101 \times 2^{-4} = 0.000110011001100110011001101$

笔者算了一下，这个数的值是 0.100000001490116119384765625 。很接近 0.1 是不是？但很遗憾，不是 0.1 ！它比 0.1 要大一丢丢，但如果我们将最后一位改成 0 ，又比 0.1 小……

进一步增加小数位数，可以使数值进一步逼近 0.1 。但由于存储小数部分的 23 个二进制位是固定，我们无法这么做。这个问题的本质在于，二进制中 1 无法被 10 整除。正如十进制中 1 无法被 3 整除一样，再多的位数也于事无补。

由于数值无法精确表示，在运算的过程中，误差会积少成多，最终可能导致重大错误：

1
2

// 这个例子是64位版本浮点数，误差比32位版本要小一些
0.1 + 0.1 + 0.1 // 0.30000000000000004

解决方案

那么，我们应该如何解决浮点数的精度问题呢？答案很简单——

对精度有要求的场景，不要使用浮点数！必须使用十进制运算类库！

很多编程语言都提供了高精度的十进制运算库，比如 Python 中的 decimal.Decimal ，Go 语言的 github.com/shopspring/decimal ，以及 JS 中的 decimal.js 。

以 Python 使用 decimal.Decimal 计算二进制小数 0.000110011001100110011001101 的值为例：

1
2
3
4
5
6
7

>>> from decimal import Decimal
>>> sum([
    Decimal(2)**-i
    for i, v in enumerate('0000110011001100110011001101')
    if v == '1'
], Decimal(0))
0.100000001490116119384765625

需要特别注意的是，由于十进制运算库无法直接利用 CPU 基于二进制位的运算能力，执行效率要比浮点数差很多。

附录

最后附上一个展示浮点数底层二进制位的 C 语言程序，有兴趣的同学可以玩一玩：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

#include <stdio.h>

void print_bits(unsigned long long value, int n) {
	for (int i=0; i<n; i++) {
		if (i>0 && i%8==0) {
			printf("-");
		}

		printf("%lld", (value>>(n-1-i)) & 1);
	}
}

void print_ieee754_layout(void *c, int bits) {
	unsigned long long value;

	int fracbits, expbits;

	if (bits == 32) {
		value = (unsigned long long)(*((unsigned int *)c));

		// 32位浮点数，小数部分为23位，指数为8位，最高位是符号位
		fracbits = 23;
		expbits = 8;
	} else {
		value = *((unsigned long long *)c);

		// 64位浮点数，小数部分为52位，指数为11位，最高位是符号位
		fracbits = 52;
		expbits = 11;
	}

	// 取数掩码
	unsigned long long fracmask = (1 << fracbits) - 1,
		expmask = (1 << expbits) - 1;

	// 分别取出各个部分
	unsigned int sign = (value >> (bits-1)) & 1;
	unsigned long long exp = (value >> fracbits) & expmask;
	unsigned long long frac = value & fracmask;

	// 分别打印
	printf("s=%u/%c", sign, sign == 1 ? '-' : '+');
	printf(" exp=");
	print_bits(exp, expbits);
	printf("/%03llu", exp);
	printf(" frac=");
	print_bits(frac, fracbits);
}

void print_float(float f) {
	printf("% 20.9f: ", f);
	print_ieee754_layout(&f, 32);
	printf("\n");
}

void print_double(double d) {
	printf("% 20.9f: ", d);
	print_ieee754_layout(&d, 64);
	printf("\n");
}

int main() {
	print_float(0.1);
	print_float(0.2);
	print_float(-0.203125);

	print_double(0.1);
	print_double(0.2);
	print_double(-0.203125);

	return 0;
}

订阅更新，获取更多学习资料，请关注我们的公众号：