前面我们介绍了 哈希索引 和 LSM树索引 ,它们都基于日志结构式的数据文件。虽然工程界对这种索引的认可度正与日俱增,但还远不是最受欢迎的索引技术。
那么,目前应用最广的索引技术又是什么呢?
您可能早就有所耳闻——这就是本文要探讨的 B树( b-tree )索引。B树可以说是数据库索引技术中的武林盟主,能够几十年长盛不衰,必定有它自己的独门秘诀。
索引结构
跟我们在 LSM树 一节中提到的 SSTable 一样,B树也是将数据组织成有序形式,因此支持范围查询。尽管如此,它们的底层结构却完全不同,B树有自己独特的设计哲学。
日志结构式索引将数据分成大小可调节的分段,通常是几兆或更大,然后再顺序写入磁盘。而B树则是以 块( block )为单位来组织数据,块大小是固定的,通常是 4KB ,也可以更大。这种设计更贴近磁盘的硬件结构,因为磁盘也是以块为单位来读写数据的。
出于性能方面考虑,计算机通常以一定字节数(如 4KB )为单位来存取数据。在不同的场景有不同的叫法:磁盘数据一般称为 块 ( block ),内存数据一般称为 页( page )。这两种场景数据库均有涉及,因而术语可以混用。
磁盘中的每个数据块都有一个唯一的地址,因此数据块间可以互相引用,有点像内存中的指针。因此,我们可以用这种方式,将数据块组织成一棵树——B树( b-tree )。
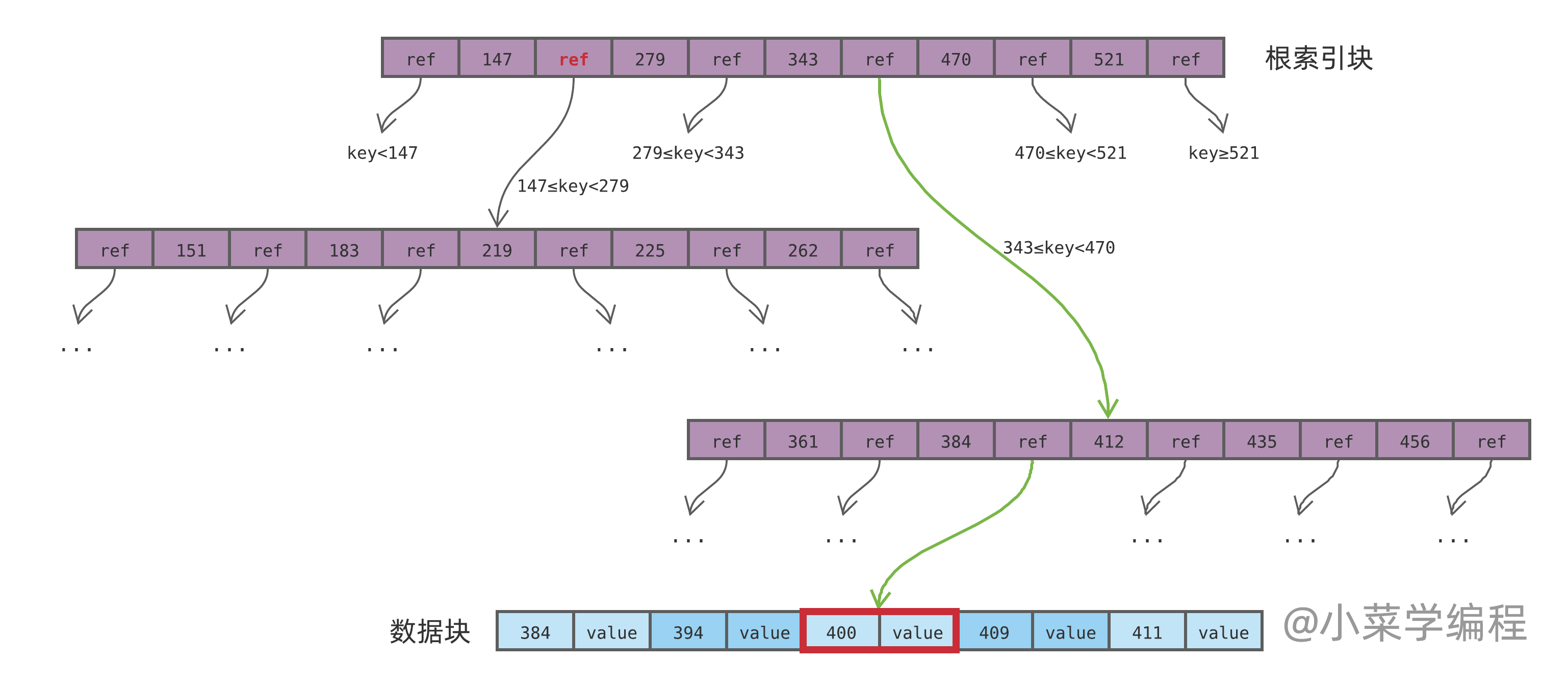
如上图,为简化讨论,我们假设数据库记录只有两个字段:一个是索引键,类型为整数;另一个是值。数据按索引键排序,依次保存在一个数据块中,如蓝色数据块所示。
紫色部分数据块为索引,它将索引键的范围划分为多个区间;每个区间保存着另一个数据块的地址( ref ),表示该范围内的数据,可以通过 ref 指向的数据块找到。上图中红色的 ref 表示,$147 \le key \lt 279$ 之间的数据,可以通过其左下方的另一个索引数据块找到。
如果子范围内的数据记录还很多,单个数据块容纳不下,ref 便指向另一个索引块,进一步将数据范围分小;如果子范围内的数据记录不多,一个数据块就能装下,ref 便直接指向数据。
这样一来,ref 就将数据块组织成一棵多叉树,数据块主要分为两种:
- 一种用于保存数据记录,如上图蓝色部分,位于树的 叶子节点 ,简称 数据块 ;
- 一种用于保存索引,如上图紫色部分,位于树的的 内部节点,简称 索引块 ;
从树的根节点索引块出发,根据数据键所在范围的 ref 逐层往下找,即可定位到数据记录。举个例子,当查询键为 400 的记录时,搜索路径如绿色箭头线所示:
- 从根索引块出发,400 落在区间 [343, 470) ,根据该区间 ref 找到下一级;
- 来到下一个索引块,400 落在区间 [384, 412) ,根据该区间 ref 找到下一级;
- 最终来到蓝色的数据块,待查找的数据记录就在里面;
范围查询
为了支持范围查询,数据库将数据记录排过序后才保存到数据块,相邻数据块间则通过双向链表指针连接在一起。
这样一来,数据库只要先定位边界元素,然后以此为起点遍历数据即可:
- 如果查询条件为小于,则从后往前遍历数据;
- 如果查询条件为大于,则从前往后遍历数据;
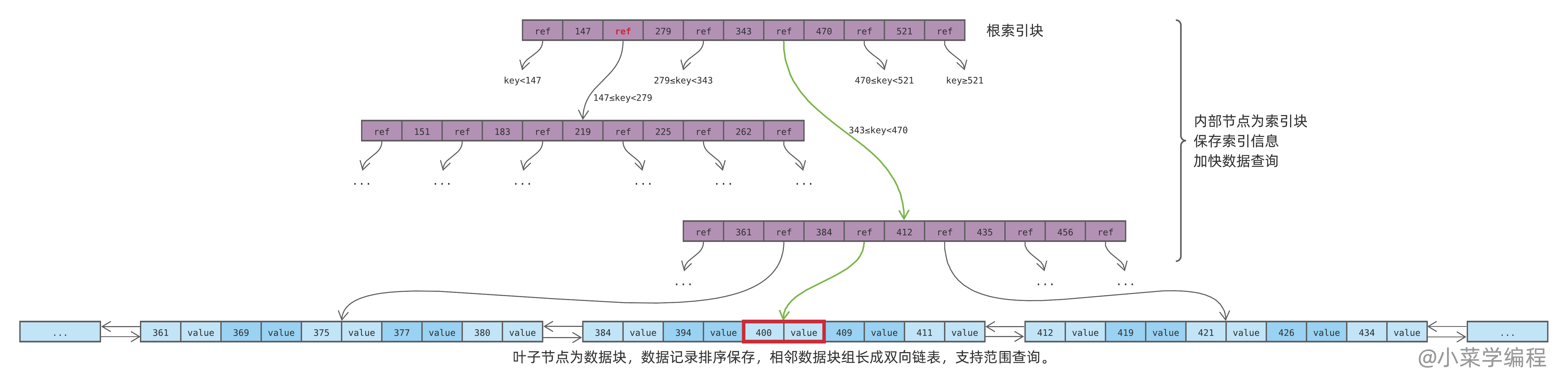
如上图,以查询大于等于 400 且小于 420 的数据为例:
- 数据库定位到键值为 400 的数据记录,如红框所示;
- 数据库检查本数据块内 400 以后的记录,满足小于 420 则取出;
- 数据库根据链表指针找到下一个数据块,继续检查里面的数据记录,满足小于 420 则取出;
- 数据库重复步骤 3 ,逐个往后遍历数据块,直到有数据记录大于等于 420 ;
分支因子
我们注意到,B树是一种多叉树。那么,为什么不能用最简单的二叉树呢?
实际上,每个树节点最多可以有多少个分叉,是树的一个非常重要的特性—— 分支因子( branching factor )。我们知道,在数据记录数一定的前提下,树的分支因子越大,高度越低。
我们使用排序树来查找数据时,从根节点开始不断搜索,最终来到叶子节点。换句话讲,我们需要检查的节点数,其实就是树的高度。
而数据库数据需要持久化并保存在磁盘里面,那磁盘有什么特点呢?
- 磁盘 IO 比较慢,非顺序的磁盘 IO 更是如此;
- 磁盘 IO 以 块( block )为数据单位,单次 IO 总是读写整个块;
在排序树中搜索数据,显然是离散读,而不是顺序读。因为我们无法保证 ref 指向的数据块就在当前块后面,磁盘通常只能重新 寻道( seek )后才能读取数据。由于磁盘寻道很慢很慢,IO 次数必须尽量减少,因此树的高度应该尽量压低。
另一方面,磁盘以块为单位读写数据,一个块可以保存很多分支信息。如果一个块只保存两个分支,那就浪费了。因为就算只保存两个分支,读的时候还是必须整块读,开销是一样的。因此,不如尽量提高分支数,这样还能减低树的高度,进而减少 IO 次数。
通常 4KB 大的数据块可以保存多达 500 个分支,如果树的高度为 3 ,可以支撑多达 $500^3=125000000$ 个数据,超过一亿。有意思的是数据库根索引块通常缓存在内存中,这样只需 2 次 IO 操作即可从超过 1 亿数据中找到想要的那个。
综上所述,B树几乎就是为磁盘量身定制的数据结构,它充分地利用了磁盘的特点:
- 磁盘以块为单位读写数据,B树就以块为节点,组织成多叉树;
- 磁盘 IO 很慢,B树就通过提高分支因子,降低树的高度,减少 IO 次数;
写操作
数据库写操作分为两种,一种是 更新( update ),一种是 插入( insert )。
如果要更新数据库中的已有记录,先搜索B树找到包含该记录的数据块(叶子节点)。然后修改数据块的记录值,再将个数据块写回磁盘。由于数据块只是内容改变了,位置不变,因此B树中任何对该数据块的引用仍然有效。
如果要插入一条新记录,同样先搜索B树,找到数据范围包含新记录的数据块(叶子节点)。如果数据块还有足够空间,就将新记录添加进入并保存到磁盘即可。如果数据块空闲空间不足,则需要将其分裂为两个:
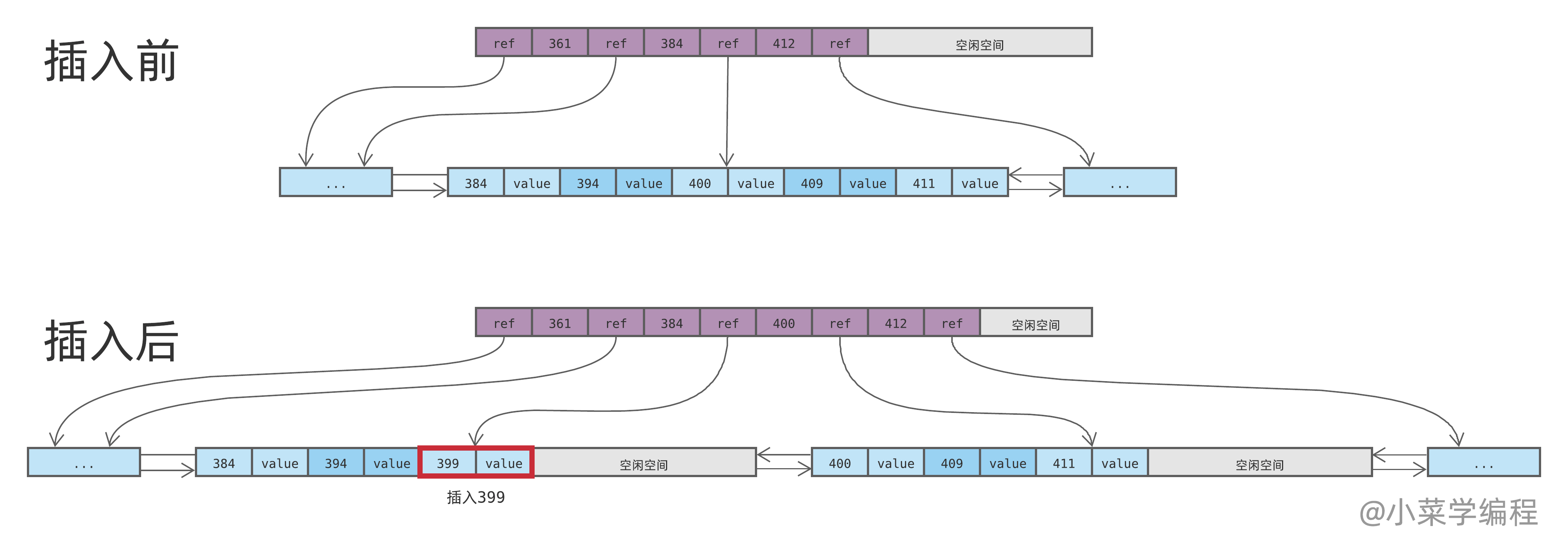
如上图,以插入 399 为例:由于目标数据块已经存满,需要将其分裂为两个。分裂后的数据块都只有一半数据,新记录保存在其中的一个。
如果新记录的键相对较小,则保存在左边的数据块;否则就保存在右边的数据块。399 跟该范围的其他数据相比较小,因此保存在左边数据块。
由于数据块发生了分裂,因此它们的父节点需要更新,以便记录最新的数据范围和分支信息。
B树算法可以保证树的 平衡( balanced ):一棵包含 $n$ 个键的B树,高度不超过 $O(\log{n})$,否则树的性能会大打折扣。通常一棵 3 层或 4 层深的B树即可容纳数据库所有数据,因此查询时无须遍历太多数据块,性能相对较好。
至此,三种主流的数据库索引技术已经全部介绍完毕。除了本节介绍的B树索引,其他两种分别是:
由于篇幅关系,不少细节有所省略。如果您还想更加深入地研究索引技术,可以翻翻《数据密集型应用系统设计》一书,一睹为快!偷偷说一句,本文也是参考这本书中的内容来写的,哈哈~
《数据密集型应用系统设计》 是后端必读经典之一,作者涵盖了数据存储和分布式系统设计的方方面面,而且写得非常通俗易懂,强烈推荐!感兴趣可以在这看看目录:
订阅更新,获取更多学习资料,请关注我们的公众号:

 小菜学编程
小菜学编程

