int 源码解析：如何实现大整数运算？

整数溢出是程序开发中一大难题，由此引发的 BUG 不计其数，而且相当隐蔽。 Python 选择从语言层面彻底解决这个痛点，殚心竭虑设计了整数对象。

上一小节，我们探索了整数对象，并初步掌握整数对象的内部结构。深入源码细节前，我们先重温整数对象的内部结构：

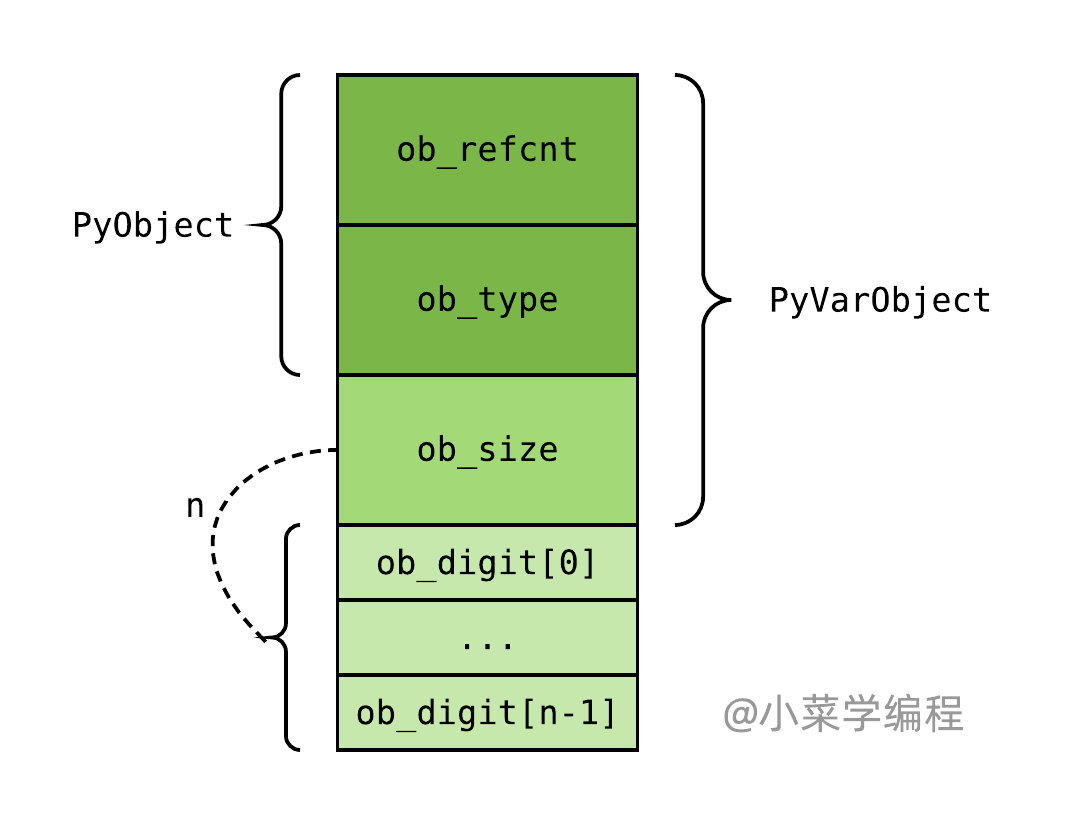
PyLongObject

  • ob_digit 为 C 整数数组，用于存储被保存整数的 绝对值 ；
  • ob_size 为 变长对象 关键字段，维护数组长度以及被保存整数的 符号 ；

Python 整数对象通过串联多个 C 整数类型，实现大整数的表示。整数对象内部包含一个 C 整数数组，数组长度与对象表示的数值大小相关，因此整数对象也是 变长对象 。

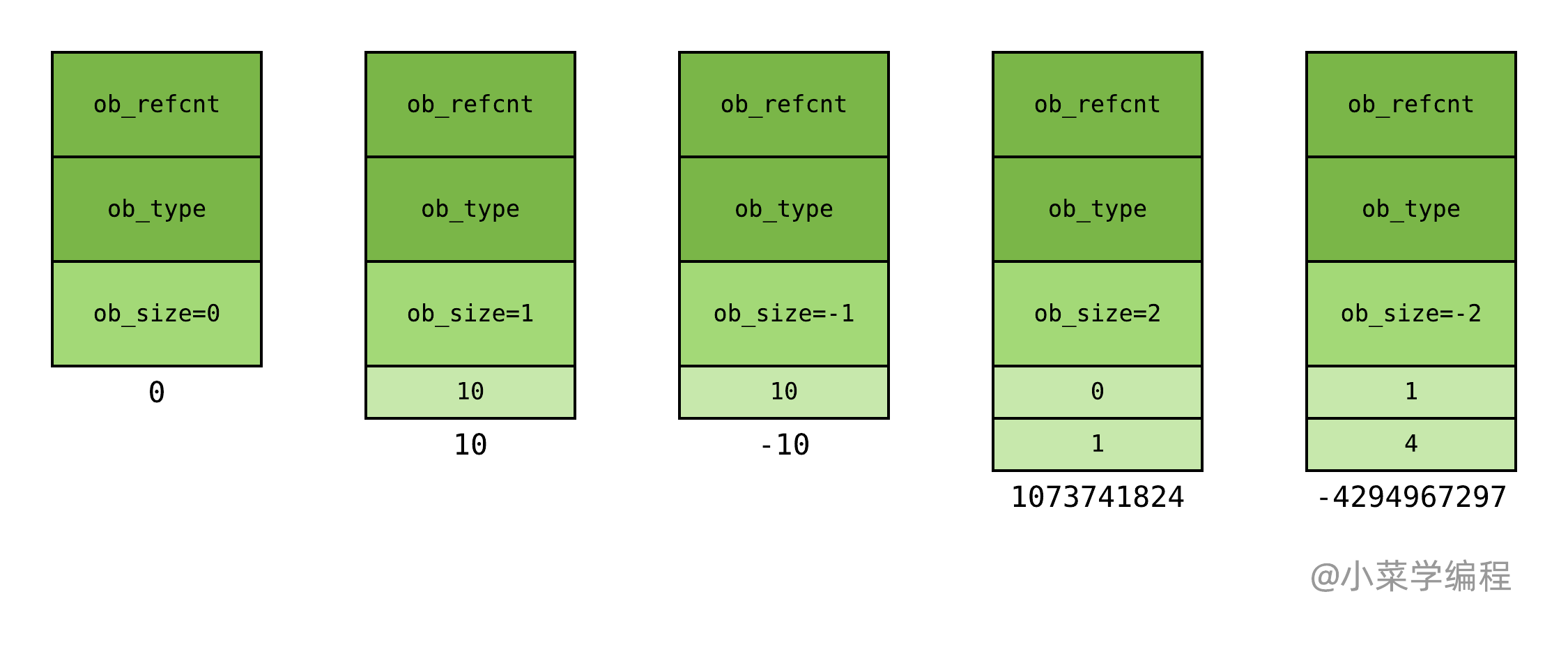
用整数数组表示大整数的思路其实平白无奇，难点在于大整数 数学运算 的实现，这是也比较考验编程功底的地方。不管是校招还是社招面试，大整数实现都是一个比较常见的考察点，必须掌握。

接下来，我们继续深入整数对象源码( Objects/longobject.c )，窥探大整数运算的秘密。

数学运算概述

根据我们在 对象模型 中学到的知识，对象的行为由对象的 类型 决定。因此，整数对象数学运算的秘密藏在整数类型对象中。我们在 Objects/longobject.c 中找到整数类型对象( PyLong_Type )，其定义如下所示：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

PyTypeObject PyLong_Type = {
    PyVarObject_HEAD_INIT(&PyType_Type, 0)
    "int",                                      /* tp_name */
    offsetof(PyLongObject, ob_digit),           /* tp_basicsize */
    sizeof(digit),                              /* tp_itemsize */
    long_dealloc,                               /* tp_dealloc */

    //...

    &long_as_number,                            /* tp_as_number */

    //...

    long_new,                                   /* tp_new */
    PyObject_Del,                               /* tp_free */
};

类型对象中， tp_as_number 是一个关键字段。该字段指向一个 PyNumberMethods 结构体，结构体保存了各种数学运算的 函数指针 。我们顺藤摸瓜，很快便找到整数对象所有数学运算的处理函数：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

static PyNumberMethods long_as_number = {
    (binaryfunc)long_add,       /*nb_add*/
    (binaryfunc)long_sub,       /*nb_subtract*/
    (binaryfunc)long_mul,       /*nb_multiply*/
    long_mod,                   /*nb_remainder*/
    long_divmod,                /*nb_divmod*/
    long_pow,                   /*nb_power*/
    (unaryfunc)long_neg,        /*nb_negative*/
    (unaryfunc)long_long,       /*tp_positive*/
    (unaryfunc)long_abs,        /*tp_absolute*/
    (inquiry)long_bool,         /*tp_bool*/
    (unaryfunc)long_invert,     /*nb_invert*/
    long_lshift,                /*nb_lshift*/
    (binaryfunc)long_rshift,    /*nb_rshift*/
    long_and,                   /*nb_and*/
    long_xor,                   /*nb_xor*/
    long_or,                    /*nb_or*/
    long_long,                  /*nb_int*/
    // ...
};

至此，我们明确了整数对象支持的全部 数学运算 ，以及对应的 处理函数 (下表仅列举常用部分)：

数学运算 处理函数 示例
加法 long_add a + b
减法 long_sub a - b
乘法 long_mul a * b
取模 long_mod a % b
除法 long_divmod a / b
指数 long_pow a ** b

最后，我们用一张图片来总结 整数对象 、 整数类型对象 以及 整数数学运算处理函数 之间的关系：

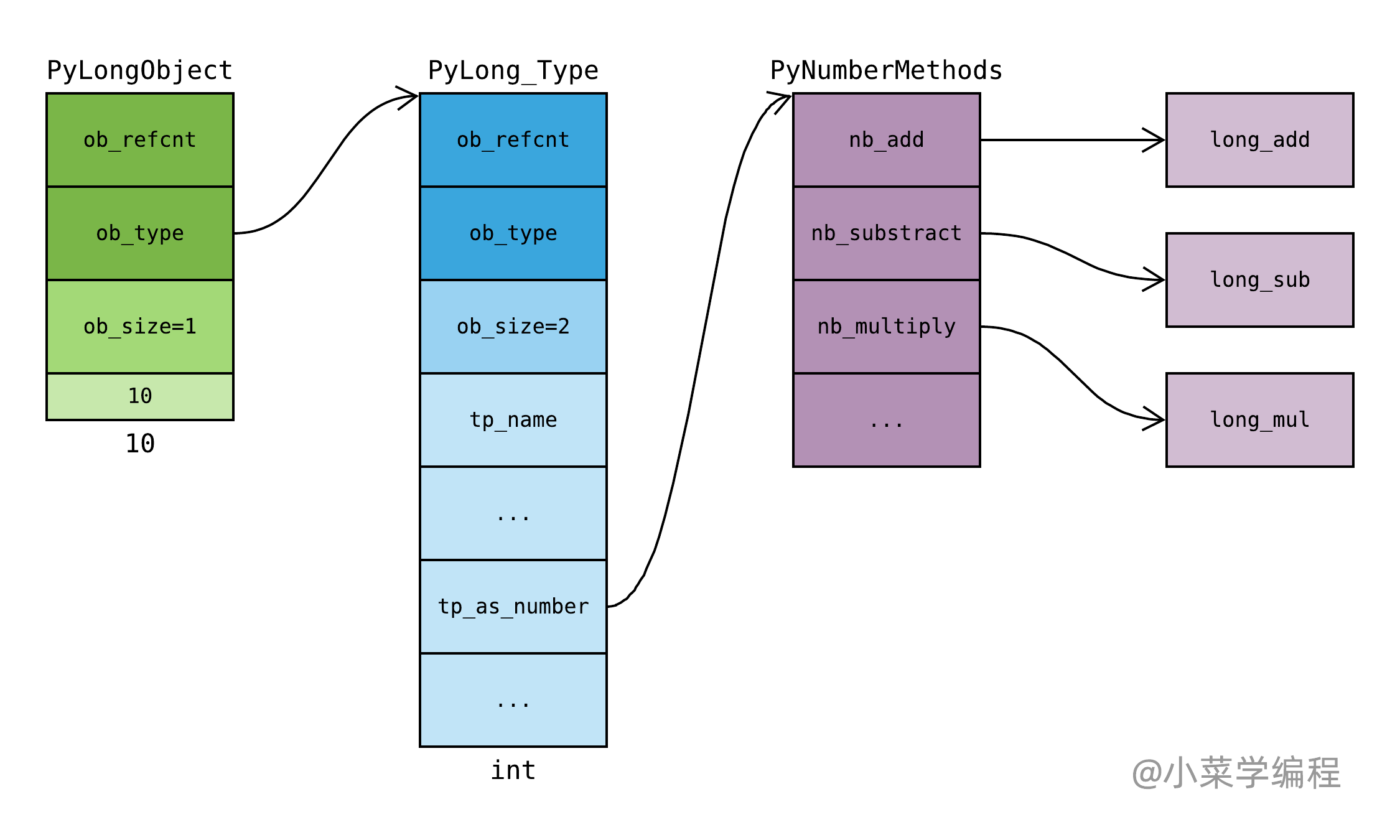
加法

如何为一个由数组表示的大整数实现加法？问题答案得在 long_add 函数中找，该函数是整数对象 加法处理函数 。我们再接再厉，扒开 long_add 函数看个究竟(同样位于 Objects/longobject.c )：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

static PyObject *
long_add(PyLongObject *a, PyLongObject *b)
{
    PyLongObject *z;

    CHECK_BINOP(a, b);

    if (Py_ABS(Py_SIZE(a)) <= 1 && Py_ABS(Py_SIZE(b)) <= 1) {
        return PyLong_FromLong(MEDIUM_VALUE(a) + MEDIUM_VALUE(b));
    }
    if (Py_SIZE(a) < 0) {
        if (Py_SIZE(b) < 0) {
            z = x_add(a, b);
            if (z != NULL) {
                assert(Py_REFCNT(z) == 1);
                Py_SIZE(z) = -(Py_SIZE(z));
            }
        }
        else
            z = x_sub(b, a);
    }
    else {
        if (Py_SIZE(b) < 0)
            z = x_sub(a, b);
        else
            z = x_add(a, b);
    }
    return (PyObject *)z;
}

long_add 函数并不长，它调用了其他辅助函数完成加法运算。

那么，long_add 函数的内部逻辑是怎样的呢？大整数的 减法 运算又是如何完成的呢？点击 阅读原文，获取更多细节！

【Python源码剖析】系列文章首发于公众号【小菜学编程】，敬请关注：

【Python源码剖析】系列文章首发于公众号【小菜学编程】，敬请关注：

fasionchan 2020-10-27