我们已经完成加法器设计,那么减法运算又该如何实现呢?
借位减法
开始研究这个问题之前,我们先来回顾减法的计算步骤。跟加法运算一样,减法也是从右往左,逐位相减。如果被减数比减数小,就得从更高位借位。我们来请看一个例子:
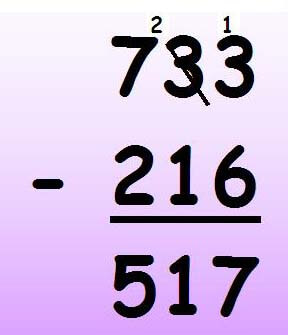
先计算个位,由于被减数个位 3 比减数 6 小,需要从十位借一位。借了一位后变成 13 ,减去 6 等于 7 。接着计算十位,由于被个位借了 1 ,只剩 2 ,再减去 1 ,得到结果为 1 。
如果左边的位为 0 ,则需要再往左边借位,举个例子:
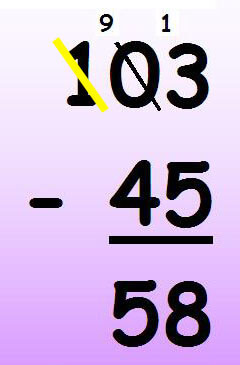
被减数个位比减数小,需要从十位借位。由于十位为 0 ,无从借起,只能从百位借位。
借位规避
由于常规减法运算需要借位,这意味着我们需要设计一个全新的减法电路。
由于减法借位跟加法进位其实非常相像,只是方向刚好相反。那么,是否能够对减法运算稍加修改,将借位改成进位,从而复用加法器的功能呢?
我们先来研究避免借位的减法运算步骤,以 $103-45$ 为例可以这样转换:
$103 - 45 = 103 - 45 + 1000 - 1000 = 103 + (999-45) + 1 - 1000$
- 我们先计算 $999-45 = 954$ ,被减数 999 每个位都是最大的,因此不用借位;
- 我们计算 $103+954+1 = 1058$ ;
- 最后我们减去 1000 ,即忽略掉千位上的借位,即可得到最终的答案 58 ;
顺便解释下几个概念:
- 999 是一个特数值,每一位均为对应进制的最大数字,位数由被减数和减数决定;
- $999-45 = 954$ ,从一串 9 减去一个数得到的数值叫做 9 的补数;
954 是 45 的 9的补数 。
二进制版本
同理,二进制减法运算亦可规避借位。只是一串 9 要换成一串 1 ,因为二进制中最大的数字是 1 。我们以 10 减去 7 为例,演示一下运算过程:
- 被减数:10 ,二进制为 1010 ;
- 减数:7 ,二进制位 111 ;
- 特数值为 1111 ,因为被减数有 4 位;
运算步骤如下:
- 对 111 求 1 的补数,即计算 $1111-111$ 的值,得到 1000 ;
- 然后跟被减数相加:$1010+1000 = 10010$ ;
- 再加上 1 :$10010+1=10011$ ;
- 最后,减去 10000 (忽略最左边的进位),即可得到最终结果 11 ,即十进制 3 ;
最后,我们再列出换算的过程,进一步加深理解:
- $1010 - 111$
- $1010 - 111 + 10000 - 10000$
- $1010 - 111 + 1111 + 1 - 10000$
- $1010 + (1111 - 111) + 1 - 10000$
请看最后一个式子,括号部分为对减数求 1 的补数,对应计算步骤①;跟被减数和 1 相加,对应计算步骤②和③;最后减去 10000 ,对应计算步骤④。
一的补数
借位规避算法需要先对减数求一的补数,因此我们需要设计一个新电路来完成这个工作。
由于 1 减去 0 结果为 1 ,减去 1 结果为零,可见结果每一位跟减数刚好相反。因此,我们只需用一排非门即可实现一补数的计算电路。电路以减数为输入,输出它的一补数:
这个电路就是所谓的 反相器( inverter ),通常可以封装成一个独立芯片。芯片包含 n 个输入和 n 个输出,每个输出和对应的输入刚好相反。
可控反相器
反相器还可以做成可控的,由一个输入端 E ( enabled )控制是否对输入取反:
- 当 E 输入 1 时,对输入进行取反,结果输出跟输入相反;
- 当 E 输入 0 时,不对输入进行取反,结果输出跟输入保持一致;
我们可以采用一排 异或门 来实现这个电路,因为异或门有这样的特性:
- 当一个输入为 0 ,输出结果跟另一个输入保持一致;
- 当一个输入为 1 ,输出结果跟另一个输入刚好相反;
以 8 位可控反相器为例,可以用 8 个异或门来实现:
控制端 E 接到每个异或的输入①,数据分别接到每个异或门的输入②,这样一来:
- 当控制端 E 输入 0 时,电路的输出结果跟输入的数据保存一致;
- 当控制端 E 输入 1 时,电路的输出结果跟输入的数据刚好相反;
由此,我们得到一个可控反相器:仅当 E 端输入 1 时,电路才对输入数据进行取反;否则原样返回。
我们为什么要制造可以控制的反相器呢?稍安勿躁,马上就可以看到它的用途了!
支持减法的加法器
我们知道,减法运算可以转化成加法运算,从而避免借位,复用加法器功能。以 $a-b$ 为例,结果为 $a + \overline{b} + 1$ ,其中 $\overline{b}$ 为减数 b 的一补数,可以通过反相器获得。因此,我们可以利用加法器来做减法运算:
- 被减数 a 接到加法器的 A 输入端(对应公式中的 a );
- 减数 b 先接到反相器求一补数,再将结果接到加法器的 B 输入端(对应公式中的 $\overline{b}$ );
- 加法器进位输入 CI 输入常量 1 (对应公式中的 1 );
这样一来,我们就在加法器的基础上,得到一个专门做减法计算的减法器。为减少冗余,我们还可以引入一个控制开关,将二者合二为一。具体怎么做呢?我们先来梳理一下加减法运算的差异:
| 运算 | A | B | CI |
|---|---|---|---|
| 加法 | a | b | 0 |
| 减法 | a | $\overline{b}$ | 1 |
- a 总是输入到加法器 A 输入端;
- b 总是输入到加法器 B 输入端,做减法时需要取反;
- 做加法运算时,加法器 CI 输入端输入 0 ,做减法运算时输入 1 ;
因此,我们可以引入一个开关 SUB ,来控制电路做加法运算还是减法运算:
- SUB 输入 0 ,表示做加法运算;
- SUB 输入 1 ,表示做减法运算;
根据上面表格,我们只需将 SUB 接到 CI ,将 b 接到可控反相器即可。可控反相器的控制端 E 由 SUB 控制,只有做减法运算时,才对 b 进行取反;否则原样返回。完整电路如下:
请注意,如果加法运算产生 CO 进位输出,代表运算结果超出和 S 的表示范围,这种情况叫做 上溢( overflow )。以 8 位加法器为例,$255 + 1 = 256$ 超过 8 位二进制数的表示范围。
此外,我们将减法运算转换成加法后,加法器必须产生 CO 进位,代表最后减去的那个数。但当减数比被减数大时,加法器就不会产生 CO 进位输出,这种情况叫做 下溢( underflow )。
因此,上面电路将加法器的进位输出 CO 和 SUB 接到一个异或门,来判断计算结果是否溢出:
| 运算 | SUB | CO | F | 备注 |
|---|---|---|---|---|
| 加法 | 0 | 0 | 0 | 正常 |
| 加法 | 0 | 1 | 1 | 上溢 |
| 减法 | 1 | 0 | 1 | 下溢 |
| 减法 | 1 | 1 | 0 | 正常 |
至此,我们得到一个更为强大的加法器,它既能做加法运算,又能做减法运算,由开关 SUB 控制。然而,它现在还不能处理负数,减数比被减数大就造成下溢异常。
下一小节,我们继续研究如何表示负数,以及如何将我们的加法器支持负数计算,敬请期待!
【小菜自制计算机】系列文章首发于公众号【小菜学编程】,敬请关注:

 小菜学编程
小菜学编程

