非对称加密算法简介及编程实践

网络

虽然对称加密算法可以胜任很多加密场景，但还是有不少特殊情况。

从前有一个黑帮，老大和手下们之间的通信必须加密确保安全。于此同时，老大希望手下发给他的信息，不能被其他手下知晓。若采用对称加密算法，只能给每个手下都分配一个独立的密钥，但老大觉得太麻烦了。该怎么办呢？

黑帮老大希望他只维护一份密钥，就能达到这样的效果，有办法做到吗？

——且看本文介绍的主角——非对称加密算法。

概念

既然我们平时所熟知的加密被称为对称加密，那么与之对应，就有 非对称加密（ asymmetric encryption ）。非对称加密，顾明思议，在加密和解密环节用的密钥是不同的。

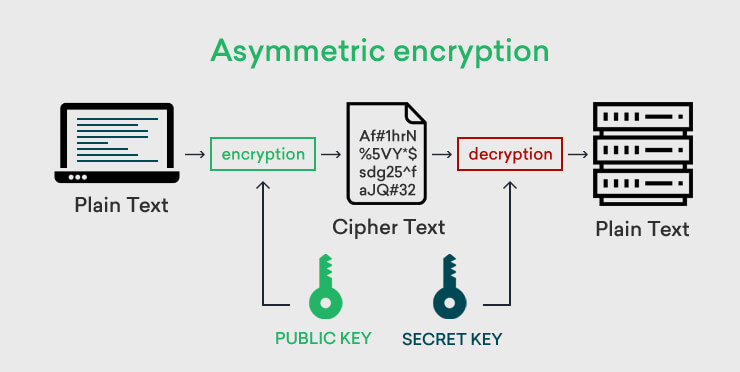
如上图，非对称加密算法需要两把不同的密钥，这两把密钥组成一对：

  • 公钥（ public key ），公钥用来对数据进行 加密 ；
  • 私钥（ private key ），也称为 密钥（ secret key ），用来对数据进行 解密 ；
  • 公钥和私钥总是成对出现，用公钥加密后得到的密文，必须用对应的私钥才能解密；

这套加密机制完美解决了黑帮老大的难题，他只需要生成一对密钥：公钥分发给手下们，他们先用公钥加密信息，再发老大；老大接到密文，就用自己保管的私钥来解密；手下们就算拿到别人发的密文也解不开，因为私钥只有他们老大才有。

神奇的数学原理

您可能会觉得公钥和私钥的加密机制非常不可思议，这一切其实来一个神奇的数学原理。

我们来做一个数字游戏，您随便写下一个整数 m （ $1 \lt m \lt 7387$ ），然后计算 $m^3 \mod {7387}$ 并把结果告诉我，我就知道您写下的整数 m 是什么！不信我们来试试，假设您写下的整数是 123 ：

1
2
3

# 用Python求123的3次方，再除以7387得到余数
>>> 123 ** 3 % 7387
6730

那么，我该如何通过结果 6730 还原出您写下的整数 123 呢？神奇的现象来了：

1
2
3

# 计算结果6730的4811次方，然后对7387取模
>>> 6730 ** 4811 % 7387
123

您还可以写下其他数字试试，同样的现象一样成立：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

# 520
>>> 520 ** 3 % 7387
3842
>>> 3842 ** 4811 % 7387
520

# 1314
>>> 1314 ** 3 % 7387
7382
>>> 7382 ** 4811 % 7387
1314

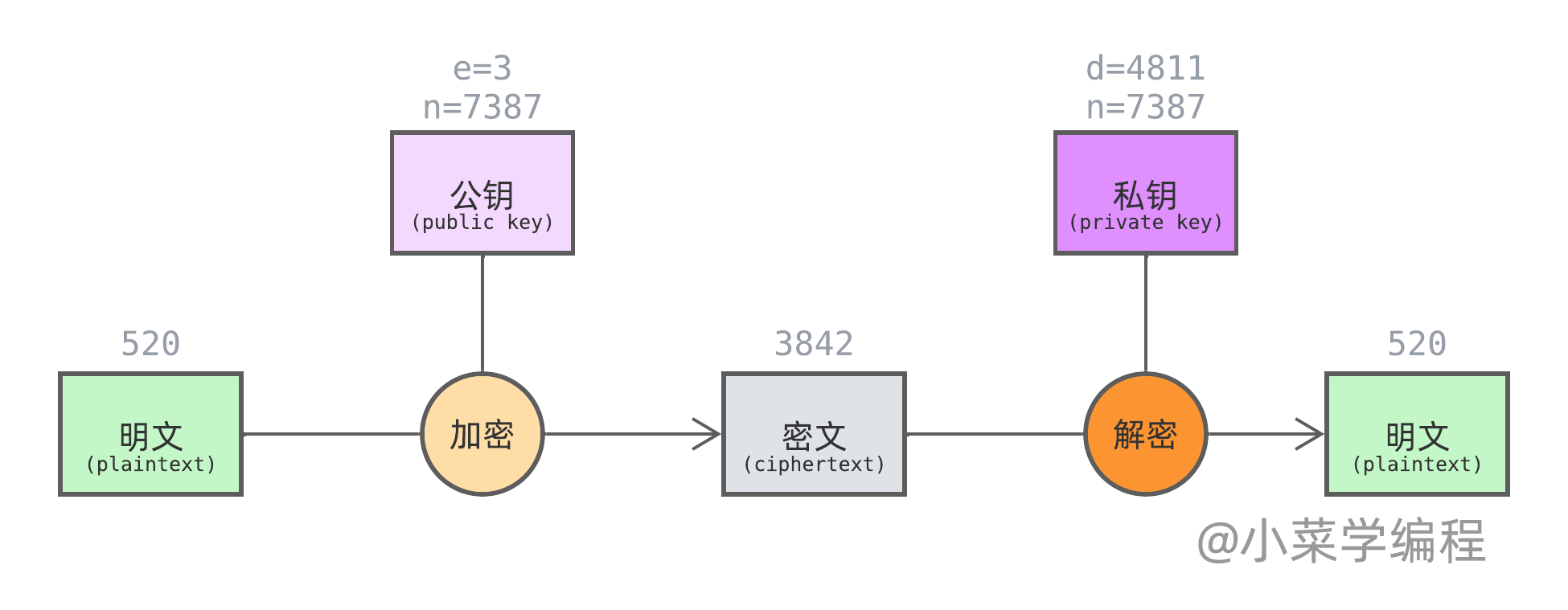
哇，太神奇了！如果把整数 520 作为待加密的数据，那么 3 和 7387 就是公钥，数据和公钥一起计算得到的结果 3842 则是密文，而 4811 和 7387 则是私钥！这个数字游戏其实就是关于公钥加密，私钥解密的故事！

那么，公钥参数 3 和 7387 ，私钥参数 4811 和 7387 又是怎么生成的呢？

第一步，随机选择两个质数 p 和 q ：

1
2

p = 83
q = 89

第二步，计算 p 和 q 的乘积 n ：

1

n = p * q = 7387

第三步，计算 n 的欧拉函数 $\phi(n)$ ，记为 phi ：

1

phi = (p-1) * (q-1) = 7216

第四步，随机选择一个整数 e ，满足 $1 \lt e \lt \phi(n)$ ，且 e 和 $\phi(n)$ 互质：

我们随机选一个质数 e ，使得 $\phi(n)$ 不能被 e 整除即可。

1
2

# 我们选一个最简单的3作为例子
e = 3

第五步，计算 e 对 $\phi(n)$ 的模反元素 d ，即找到一个数 d 使得 ed 除以 $\phi(n)$ 的余数为 1 ：

$ed \equiv 1 \pmod {\phi(n)}$ 等价于

$ed - 1 = k\phi(n)$

这个方程据说可以用扩展欧几里得算法来求解，但小菜没空去复习，就写了个函数暴力求解：

1
2
3
4

def findD(e, phi):
    for d in itertools.count(e+1):
        if (e*d-1) % phi == 0:
            return d

这几行代码对于给定的 e 和 $\phi(n)$ ，以 e+1 为起点，逐一尝试 d 的值。如果 ed-1 刚好能够被 $\phi(n)$ 整除，便意味着我们找到合适的 d 。这个例子合适的 d 值为：4811 。

我还写了一个 Python 脚本来生成公钥和私钥参数，有兴趣的话可以自己玩一玩：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

import bitmap
import itertools
import random

def getPrimes(limit=2**16-1):
    size = limit + 1

    m = bitmap.BitMap(size)
    for i in range(2, size//2+1):
        for j in itertools.count(2):
            pos = i*j
            if pos < size:
                m.set(pos)
            else:
                break

    primes = []
    for i in range(2, size):
        if not m.test(i):
            primes.append(i)

    return primes

def findD(e, phi):
    for d in itertools.count(e+1):
        if (e*d-1) % phi == 0:
            return d

# 生成质数
primes = getPrimes(2**16-1)

# ①随机选两个质数p和q
p = random.choice([i for i in primes if i < 100])
print('p:', p)

q = random.choice([i for i in primes if i < 100 and i != p])
print('q:', q)

# ②计算p和q的乘积n
n = p * q
print('n:', n)

# ③计算n的欧拉函数phi
phi = (p-1) * (q-1)
print('phi:', phi)

# ④找到一个比phi小的数e，使得e和phi互质
# 我们找一个质数e，使得phi不能被e整除
e = [p for p in primes if phi%p][0]
print('e:', e)

d = findD(e, phi)
print('d:', d)

# 验证
for m in range(2, n):
    c = m**e % n
    m2 = c**d % n
    if m!=m2:
        print('FAILED:', m, c, m2, m==m2)

安全性

至此，游戏中的公钥 e 和 n ，私钥 d 和 n 便全部备齐！至于原理和数学证明，需要数论的一些知识，本文就不再赘述了。有兴趣的读者，可以自行查阅一些资料。

您可能对安全性还有疑问，私钥中的关键参数 d 是否有可能被破解出来呢？想要计算 d ，必须知道 $\phi(n)$ ；而想要得到 $\phi(n)$ 必须知道 p 和 q ；而想要知道 p 和 q ，必须对 n 进行因式分解。

而对极大整数 n 做因素分解是非常困难的，这决定的 RSA 算法的可靠性。我们玩的数字游戏数值都不大，很容易被破解。但只要 n 的位数足够长，被破解的可能性就非常小。同理，第三方知道加密后的密文 c 以及 密钥 e 和 n ，也很难破解出原文 m 。

这里提到的位是指二进制位，即 n 的二进制形式所占的比特位个数。

目前，能够被破解的 n 最大位数是 768 位，因此有人开始质疑 1024 位密钥的安全性。现在推荐的密钥长度至少要 2048 位，只要长度足够，安全性完全不用担心。

应用场景

加密

公钥加密私钥解密是非对称加密算法最典型的应用场景，特别适用于密钥需要公开的场景，比如 传输层安全协议 TLS ，它为通讯双方提供可靠的加密连接。

如果没有非对称加密算法，TLS 将无法实现。因为对称加密算法要求双方使用同一密钥，加密连接建立之前，只能明文协商密钥。试想浏览器想跟服务器建立安全连接，无论是它选定密钥然后发给服务器，还是服务器选定密钥发给它，只要密钥经过明文传输，加密就失去意义。

有了非对称加密算法，服务器可以生成一对密钥，私钥自己保管，公钥可以公开。当浏览器请求建立加密连接时，服务器可以将公钥发给浏览器，因为公钥是可以公开的。浏览器将敏感信息用公钥加密后再发给浏览器，只有掌握私钥的服务器才能解密，他人便无法知晓。

同理，服务器想发敏感信息给客户端，必须由客户端生成的公钥加密。换句话讲，每对密钥解决一个方向的加密问题，通讯双方都需要生成自己的密钥对，负责加密对方发来的数据。

由于非对称加密算法运算复杂，加密效率不高，通常只是用来加密少量的关键信息，比如协商密钥。回到 TLS 这个例子，其实可以借助非对称加密算法协商密钥，从而直接使用更高效的对称加密算法来加密数据：

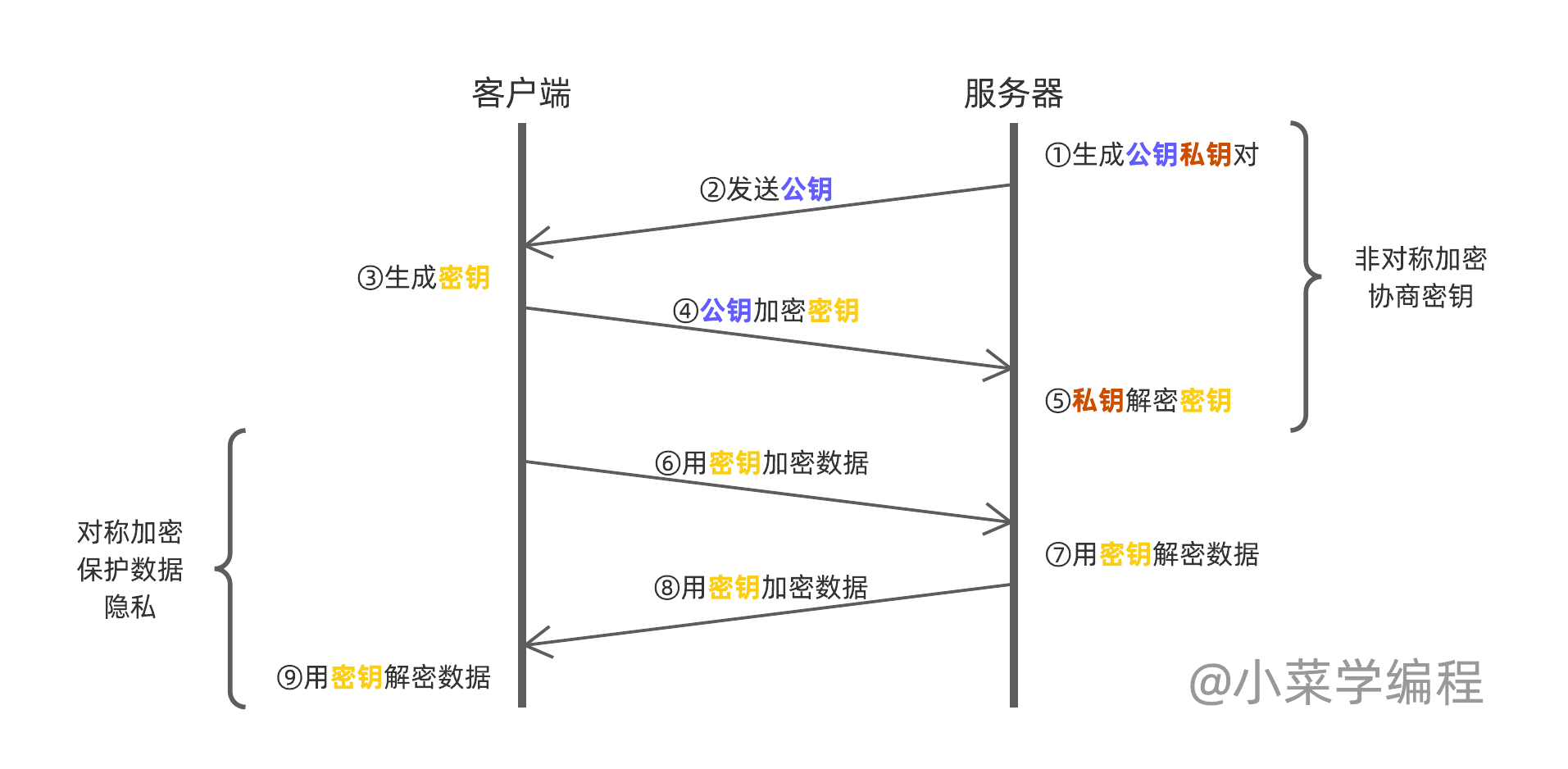
  1. 服务器生成公钥（紫色）和私钥（红色）对；
  2. 客户端（浏览器）连接上来后，服务器将公钥发给客户端；
  3. 客户端随机生成一个用于对称加密（ AES ）的密钥（黄色）；
  4. 客户端用公钥对生成的密钥进行加密，然后后发给服务器；
  5. 服务器收到客户端用公钥加密的密钥后，用自己的私钥解密，至此密钥协商完毕；
  6. 由于私钥只有服务器才有，因此第三方无法知晓客户端选定的密钥是啥；
  7. 此后通信双方采用对称加密，以该密钥加密数据；

签名

实际上，私钥也可以用来加密数据，加密后的密文只有公钥才能解密。尽管如此，由于公钥是公开的，因此这个机制不能来加密数据，但可以对用来对数据进行签名防伪。

回到黑帮的场景，老大会给手下们发指令。虽然指令内容可以公开，但是必须有一个机制来甄别指令是否老大发出的。这时应该怎么做呢？

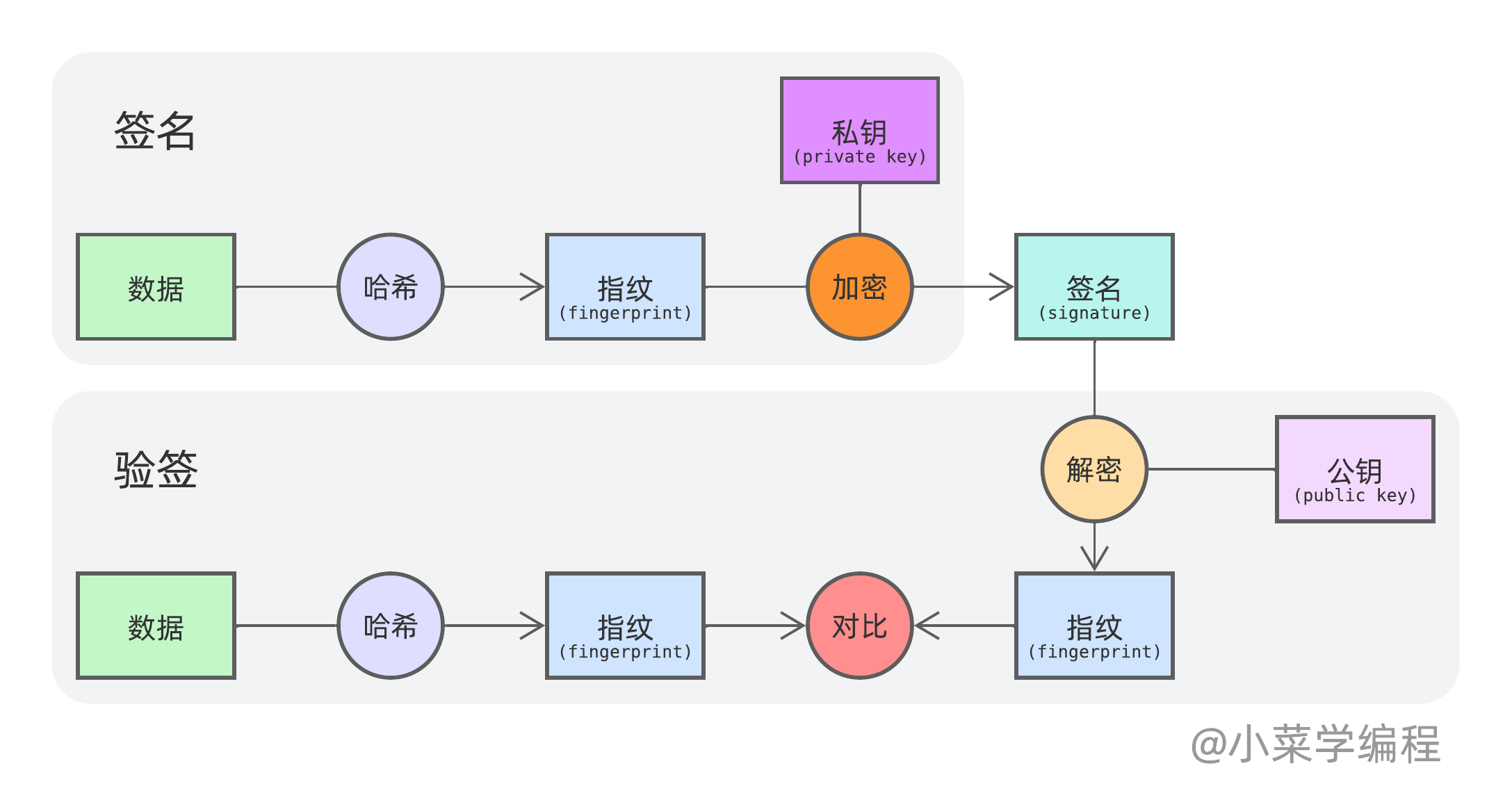
  1. 黑帮老大对指令 m 的内容计算 SHA 数据指纹，结果为 h ；
  2. 黑帮老大使用私钥对数据指纹 h 进行加密，结果作为指令的签名 s ；
  3. 黑帮老大将指令 m 和签名 s 一起发给手下；
  4. 手下重新计算指令 m 的数据指纹，与 s 解密后的结果进行对照，即可判断真伪；
    • 如果两者一致，说明指令是真实的；
    • 否则两者不一致，说明指令是伪造的；
    • 由于签名需要私钥参与，因此第三方无法伪造签名；

代码实现

最后，我们以 Go 语言为例，演示如何编程实现非对称加密、解密、签名以及验签：

密钥生成

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

// 随机生成一对密钥
key, err := rsa.GenerateKey(rand.Reader, 2048)
if err != nil {
	panic(err)
}

// 序列化公钥
publicBytes, err := x509.MarshalPKIXPublicKey(&key.PublicKey)
if err != nil {
	panic(err)
}

// 编码公钥
publicKey := pem.EncodeToMemory(&pem.Block{
	Type:  "RSA PUBLIC KEY",
	Bytes: publicBytes,
})
fmt.Println(publicKey)

// 编码私钥
privateKey := pem.EncodeToMemory(&pem.Block{
	Type:  "RSA PRIVATE KEY",
	Bytes: x509.MarshalPKCS1PrivateKey(key), // 序列化私钥
})
fmt.Println(privateKey)

加密解密

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25


// 例子直接生成一对新的密钥进行实验
key, err := rsa.GenerateKey(rand.Reader, 2048)
if err != nil {
	panic(err)
}

// 待加密明文
plaintext := []byte("fasionchan.com")

// 用公钥加密，得到密文
ciphertext, err := rsa.EncryptPKCS1v15(rand.Reader, &key.PublicKey, plaintext)
if err != nil {
	panic(err)
}

// 用私钥解密，得到原来的明文
text, err := rsa.DecryptPKCS1v15(rand.Reader, key, ciphertext)
if err != nil {
	panic(err)
}

if bytes.Compare(text, plaintext) != 0 {
	panic("error")
}

签名验签

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

// 例子直接生成一对新的密钥进行实验
key, err := rsa.GenerateKey(rand.Reader, 2048)
if err != nil {
	panic(err)
}

// 待签名数据
data := []byte("fasionchan.com")

// 对数据求哈希
dataHash := sha256.Sum256(data)

// 使用私钥对哈希值进行加密，结果作为数据签名
signature, err := rsa.SignPKCS1v15(rand.Reader, key, crypto.SHA256, dataHash[:])
if err != nil {
	panic(err)
}

// 使用公钥对签名进行解密，与哈希值对比，验证签名是否真实
if err := rsa.VerifyPKCS1v15(&key.PublicKey, crypto.SHA256, dataHash[:], signature); err != nil {
	panic(err)
}

【小菜学网络】系列文章首发于公众号【小菜学编程】，敬请关注：

【小菜学网络】系列文章首发于公众号【小菜学编程】，敬请关注：

fasionchan 2023-01-14